La curva ROC para detectar falsas alarmas del sistema

Uno de estos sistemas es la curva ROC (Receiver Operating Characteristic), y hoy veremos en qué consiste y sus aplicaciones. 

Estas abarcan diferentes ámbitos, pero los sistemas mencionados se usan principalmente para la seguridad informática y la medicina. En concreto, para identificar ciberataques o enfermedades, respectivamente, y para minimizar falsas alarmas. 

Si quieres aprender más sobre este tipo de herramientas, te recomendamos cursar el Bachelor Online en Data Science de la Universitat Carlemany. Una vez lo completes, podrás gestionar, procesar y analizar grandes cantidades de datos, con la aplicación de diferentes herramientas y tecnologías. 

Qué es la curva ROC y para qué sirve

La curva ROC es una representación gráfica de la sensibilidad que hay, en los sistemas de clasificación binaria, ante las falsas alarmas. Su construcción se basa en dos métricas principales: 

• La tasa de verdaderos positivos o TPR. 

• La tasa de falsos positivos o FPR. 

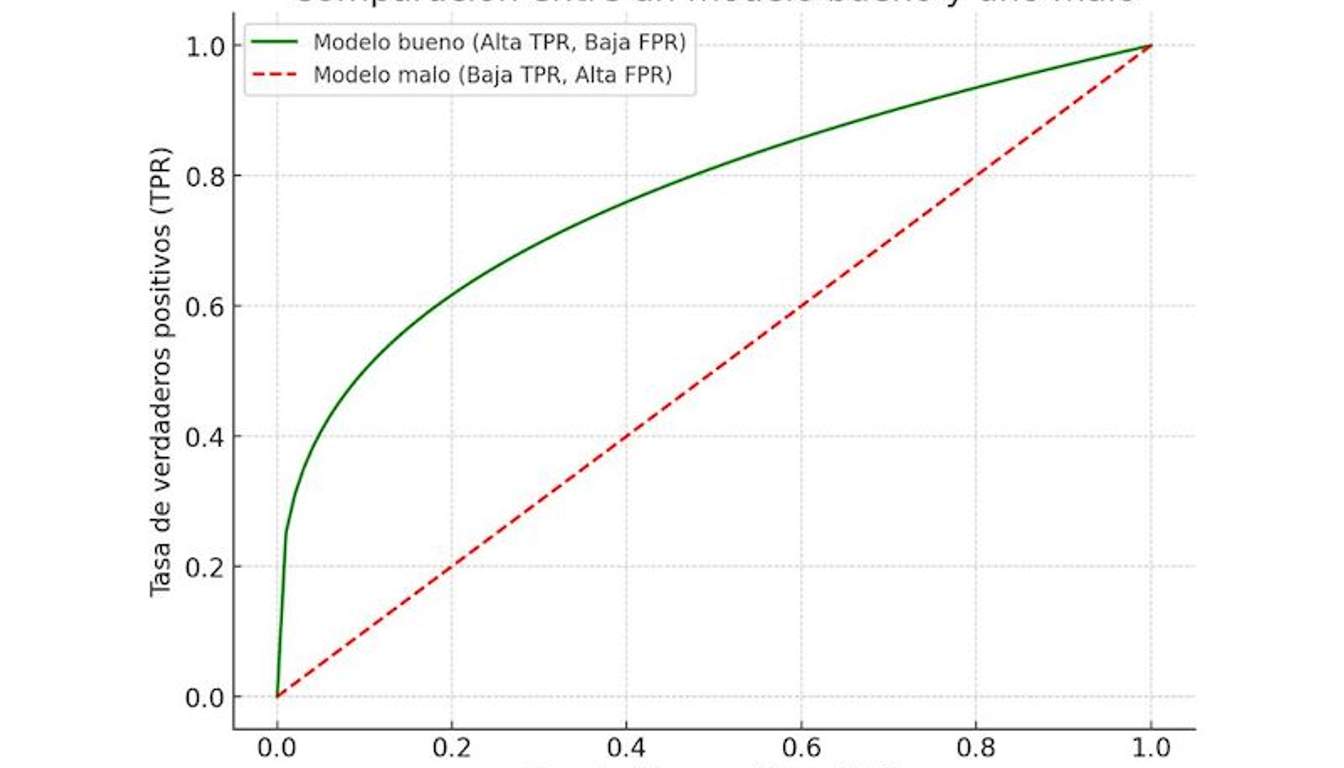
La TPR se encarga de medir la proporción de casos positivos que son identificados correctamente por el modelo. Por el contrario, la FPR representa la proporción de casos negativos que fueron clasificados como positivos, pero que en realidad no lo eran. Por tanto, se trató de un error.

En el gráfico de la curva ROC, se traza la relación que hay entre estas dos tasas por medio de distintos umbrales de clasificación. Al poder visualizar los errores con mayor facilidad, los analistas pueden comprender mejor cuál es el rendimiento del modelo en concreto, y cómo varía en función de dichos umbrales. 

Para que un modelo sea considerado como bueno, su TPR debe ser alta, mientras que la FPR baja:

Desde el punto de vista práctico, la curva ROC sirve para:

• Evaluar la capacidad discriminatoria que tiene un modelo.
• Comparar el rendimiento entre distintos modelos de clasificación.
• Identificar el umbral óptimo que permite maximizar la eficacia del modelo en un contexto determinado.

Cuál es su origen y cómo se interpreta

El uso de la curva ROC se remonta a los años 40. Durante la Segunda Guerra Mundial, se usó en el campo de la detección de señales para analizar el desempeño de sistemas de radar que identificasen aeronaves. Con el paso del tiempo, este concepto pasó a usarse también en la estadística y en el aprendizaje automático. Dentro de este último, se usa para evaluar los modelos en situaciones de clasificación binaria.

 

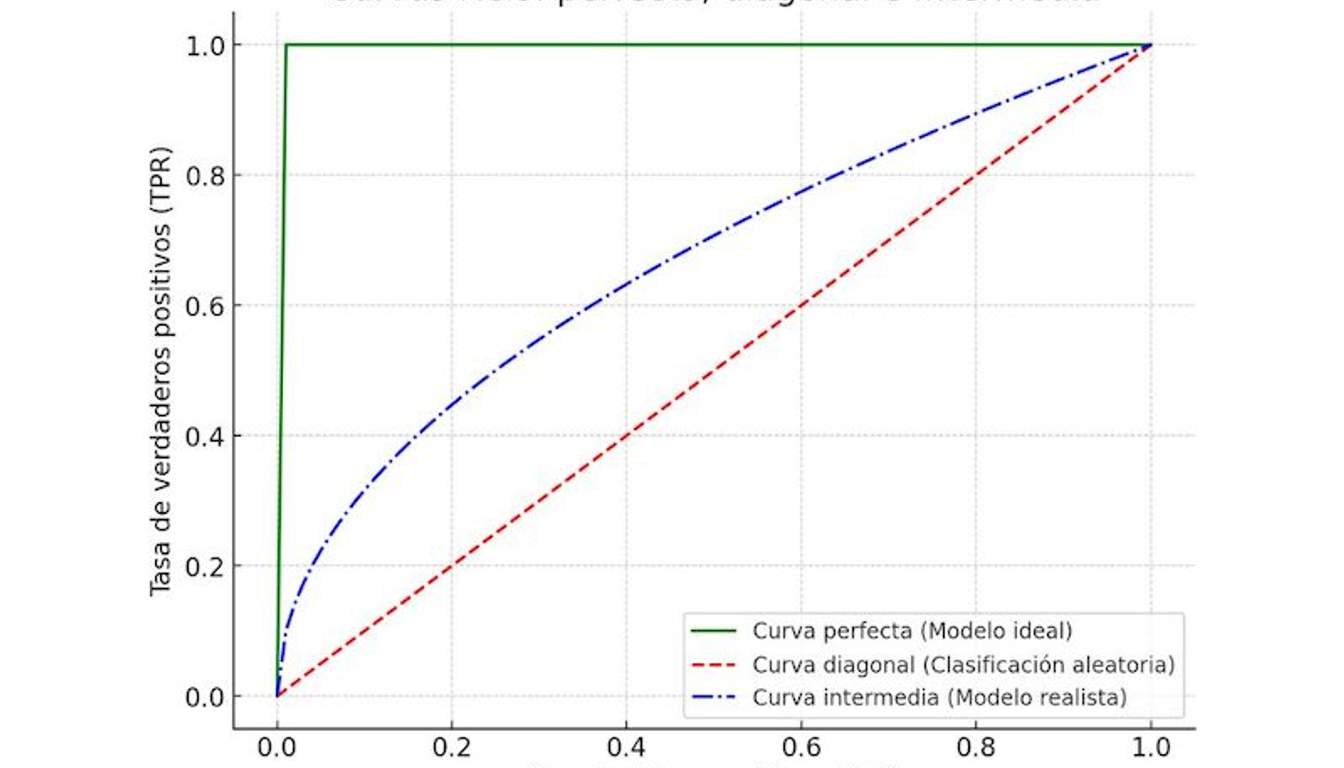
Para su interpretación, hay que observar la forma y el área bajo la curva (AUC). A la hora de elegir el modelo más adecuado, los analistas deben tener en cuenta cuáles son sus necesidades concretas. Las posibilidades en el resultado son las tres siguientes:

• Curva perfecta

  La curva idónea sería aquella que tiene una TPR=1 y una FPR=0 para todos los umbrales. En esta situación, la curva alcanzaría el ángulo superior izquierdo y después seguiría el eje superior. 

• Curva diagonal

  Si la curva tiene una inclinación de unos 45º, se interpreta que el modelo no tiene capacidad discriminatoria. Es decir, que sería similar a una clasificación aleatoria.

• Curva intermedia

  En este caso, cuanto más alejada esté la curva de la diagonal y más cerca del ángulo superior izquierdo, mejor será el rendimiento del modelo.

Área bajo la curva (AUC)

El área bajo la curva ROC, o AUC si usamos las siglas en inglés, es una medida cuantitativa que resume el rendimiento de un modelo en un solo valor. Permite a los analistas cuantificar el grado en el que un modelo puede distinguir entre clases positivas y negativas. Este indicador oscila entre 0 y 1, y su interpretación es la siguiente:

• AUC = 1. Este resultado indica que se trata de un modelo perfecto, que discrimina sin errores entre clases.
• AUC = 0.5. En este caso, el modelo realiza una clasificación aleatoria.
• AUC < 0.5. En esta tercera opción, el modelo tiene un rendimiento peor que en la clasificación aleatoria. Por tanto, podría haber errores graves en el diseño o en los datos.

El uso del AUC como métrica tiene varias ventajas:

• Independencia del umbral

  Para evaluar el rendimiento de un modelo, puede tener en cuenta todos los posibles umbrales de clasificación.

• Facilidad de comparación

  Compara el rendimiento de diferentes modelos de una forma sencilla y visual. 

• Fiabilidad

  Es menos sensible al desequilibrio de clases que otras métricas, como la precisión o la exactitud.

Aplicaciones actuales de la curva ROC

La curva ROC tiene aplicaciones principalmente en el campo de la informática y en la medicina. Pero, igual que este uso fue posterior al originario, hoy en día sus aplicaciones también se han ido diversificando. Son las siguientes:  

Ámbito médico

En medicina, la curva ROC se usa para evaluar el rendimiento de pruebas diagnósticas y modelos predictivos. Por ejemplo, puede determinar la sensibilidad en pruebas como mamografías y biomarcadores, por lo que facilita el diagnóstico de enfermedades como el cáncer. 

Seguridad informática

En informática, este sistema sirve para probar la fiabilidad de los sistemas de detección de intrusos y antivirus, que deben distinguir entre actividades normales y maliciosas. La curva ROC ayuda a ajustar estos modelos para que los falsos positivos, que serían las alertas erróneas y los falsos negativos o amenazas no detectadas, sean las más bajas posibles. 

Marketing digital

En el marketing, la curva ROC evalúa modelos de clasificación que predicen la probabilidad de que un cliente realice una compra o abandone una suscripción. Con esta información, se pueden optimizar las campañas y los recursos para incrementar la probabilidad de que consigan su objetivo. 

Investigación académica

En investigaciones donde se desarrollan nuevos algoritmos de clasificación, la curva ROC sirve para medir el impacto y la eficacia de dichos algoritmos, en comparación con otros métodos existentes.

Puesto que se trata de una herramienta muy versátil y con diferentes aplicaciones, la curva ROC es esencial en el campo de la ciencia de datos. Con la información que se obtiene, se pueden tomar decisiones en contextos críticos, como serían el diagnóstico de enfermedades o los virus e intrusos en los sistemas informáticos.

Para aprender a utilizarla y conocer otras herramientas con una finalidad similar, inscríbete en nuestro Bachelor en Data Science y conviértete en un profesional del análisis y la gestión de datos.